Como todas as ciências, a matemática foi sendo desenvolvida através dos tempos com a intenção de suprir as necessidades do homem. E nós, hoje, estudantes da matemática não poderíamos entender os vários conceitos matemáticos sem antes, ao menos, tomar ciências sobre a vida de certos sábios e seus pensamentos, que deram origem à matemática que conhecemos hoje.
Na verdade a abordagem a seguir é sobre um assunto que envolveu vários sábios durante vários séculos passados, mas começaremos nossa apresentação com o pensamento de uma das mentes mais sábias que já houve no mundo.
“A Matemática é o alfabeto com o qual Deus escreveu o universo”.Galileu Galilei
2. Surgimento
No Egito, as pirâmides de Gizé foram construídas seguindo uma certa razão em sua estrutura. A razão entre a altura de uma face e a metade do lado da base da grande pirâmide é igual a um certo número: 1,618...
Já no Papiro de Ahmes que é datado de aproximadamente 1650 a.C., encontramos um texto matemático na forma de manual prático que contém 85 problemas copiados em escrita hierática pelo escriba Ahmes de um trabalho mais antigo. Este papiro refere-se a uma “razão sagrada”.
Para entendermos melhor de que razão estamos falando, relembraremos um dos maiores matemáticos que já tivemos, Pitágoras, este que um dia disse: “Tudo na natureza é número”, e ele estava certo. Pois foi sua sociedade, composta de estudiosos de todas as ciências, artes e música, os pitagóricos, que observou a aparição desta razão entre várias obras da antiguidade, mas acima de tudo na natureza e na matemática.
Acreditavam que se quiséssemos dividir um seguimento AB em duas partes, teríamos uma infinidade de maneiras de o fazer, mas existe, no entanto, uma forma que parece ser mais agradável à vista, como se produzisse uma operação harmoniosa para os nossos sentidos, e esta seria o seguinte:
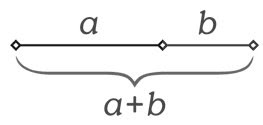
Observaremos que neste seguimento, a razão entre o maior pedaço e o segmento inteiro é a mesma entre o pedaço menor e o pedaço maior. Assim chegamos a seguinte conclusão: Assim substituindo temos
Assim substituindo temos Logo, resolvendo a equação, encontramos duas raízes
Logo, resolvendo a equação, encontramos duas raízes A raiz positiva encontrada é justamente a representação numérica desta razão, que por aparecer diversas vezes nos estudos dos pitagóricos nomearam-no PHI (φ) Letra grega, em homenagem a Phídeas, arquiteto que construiu o Partenon Grego, uma das construções mais antigas encontrada na Grécia, datada por volta de 447 e 433 a.C. Este monumento foi construído com esta razão entre vários pontos da construção, entre sua pilastras na fachada e em muitos pontos dentro do ambiente. Assim temos
A raiz positiva encontrada é justamente a representação numérica desta razão, que por aparecer diversas vezes nos estudos dos pitagóricos nomearam-no PHI (φ) Letra grega, em homenagem a Phídeas, arquiteto que construiu o Partenon Grego, uma das construções mais antigas encontrada na Grécia, datada por volta de 447 e 433 a.C. Este monumento foi construído com esta razão entre vários pontos da construção, entre sua pilastras na fachada e em muitos pontos dentro do ambiente. Assim temos 

Os pitagóricos, em seus estudos em geometria verificaram surpreendentes descobertas: No decágono regular inscrito na circunferência, a razão entre o lado do decágono e o raio da circunferência é justamente o número φ.
No pentágono regular esta razão também se repetem inúmeras vezes. Veremos nos exemplos abaixo:
Figura 01

Figura 02
Traçando todas as diagonais do pentágono regular, poderemos observar que: na figura 01 o triângulo destacado tem seus lados em relação dourada com a base, já na figura 02 o triângulo destacado tem sua base em relação dourada com os lados. O pentagrama é uma das construções geométricas que mais fascinou os estudiosos em todos os tempos. Há uma inumerável quantidade de relações douradas em sua construção. O que, é claro, chamou muita a atenção dos pitagóricos, que tornaram o pentagrama símbolo de sua sociedade, relacionando o dodecaedro (poliedro formado de 12 pentágonos regulares) com a divindade. Pois acreditavam que os poliedros mais fantásticos que descobriram tinham sua relação com a natureza.
Um tópico muito interessante, do número de ouro, relacionado com os pitagóricos, foi que não conseguiram expressar numericamente a razão entre o lado do pentágono regular e o lado do pentágono estrelado inscritos numa circunferência (que é justamente o número φ=1,618...). Quando chegaram a esta conclusão, ficaram muito espantados, pois isto era contrário a toda lógica que conheciam, e por isto o chamaram de irracional. Assim o número de ouro foi o primeiro número irracional que se teve consciência.
3. A razão de Ouro na Geometria, na Arte e na Natureza

É também no retângulo de ouro que conseguimos representar a espiral logarítmica, encontrada nos seres da natureza:
A partir deste retângulo foram observadas várias obras de arte que foram produzidas utilizando a razão de ouro. Leonardo Da Vinci foi criador de várias obras que tinham o embasamento na razão áurea. A mais conhecida delas foi à famosa Mona Lisa, que apresenta o retângulo de ouro em múltiplos locais: (a) desenhando um retângulo à volta da face, o retângulo resultante é um retângulo de ouro; (b) dividindo este retângulo por uma linha que passa na altura dos olhos, o novo retângulo também é áureo e (c) as dimensões do quadro também representam a razão de ouro.

Leonardo Utilizou bem a razão áurea na representação do padrão de beleza do ser Humano, acreditava-se que era belo ter a razão de ouro entre os membros de seu corpo. E Da Vinci representa isto muito bem em outra obra com nome de Homem Vitruviano. Onde são representadas as proporções humanas: (a) a altura do corpo humano e a medida do umbigo até o chão; (b) a altura do crânio e a medida da mandíbula até o alto da cabeça; (c) a medida da cintura até a cabeça e o tamanho do tórax; (d) A medida do ombro à ponta do dedo e a medida do cotovelo à ponta do dedo; (e) O tamanho dos dedos e a medida da dobra central até a ponta; (f) a medida da dobra central até a ponta e da segunda dobra até a ponta; (g) a medida do seu quadril ao chão e a medida do seu joelho ao chão.
Na arte, o período que mais se utilizou à razão de ouro, foi o renascentista. Também encontramos a razão dourada em outros quadros da época. Como por exemplo: (a) “O nascimento de Vênus” de Botticelli, onde Afrodite esta desenhada seguindo as proporções áureas; (b) “O sacramento da última ceia” de Salvador Dali, onde as dimensões do quadro estão na razão de ouro entre si.
Já na matemática não é só na geometria, que encontramos esta razão. Leonardo de Pisa, ou Fibonacci, como é mais conhecido, criou uma seqüência muito conhecida hoje, que representava a reprodução de coelhos na época.
Nesta seqüência, se dividirmos cada termo pelo anterior, a partir, do terceiro termo, verificamos que o resultado dessas divisões se aproxima cada vez mais do número de ouro, ou seja, o resultado tende à φ.
Na natureza encontramos vários espirais, já mencionados acima, mas também podemos encontrar e razão dourada nas sementes no centro de um girassol, nos escamas de peixes e em muitos outros animais e vegetais.
4. Efeitos
Algumas correntes místicas acreditam que objetos cujas dimensões sejam relacionados a φ, harmonizam-se com a Glândula Pineal, o que provocaria ou estimula uma sensação de beleza e harmonia no ser humano.
5. Conclusão
O número de ouro é considerado por muitos estudiosos um símbolo de harmonia. Pode ser encontrado em nosso cotidiano, de forma real e em muitos monumentos históricos. Aparece na natureza, na arte, a arquitetura, música e nos seres humanos. Por representar tudo o que o ser humano mais aprecia, foi chamado “de ouro”.

3 comentários:
Fernanda,
excelente trabalho nesta postagem.
Um grande abraço,
Alex
Oi!
Encontrei um erro, o certo seria, a/(a+b) = b/a.
E o texto concerteza está resumido demais, alguns pontos não estão claros!
é isso, abraço !
Os links relacionados com o trabalho, estão abaixo, para qualquer esclarecimento. São trabalhos já realizados na área, de onde foram retiradas todas as informações do Seminário.
www.expoente.com.br/professores/kalinke/projeto/aurea.htm
www.mat.uel.br/geometrica/artigos/ST-15-TC.pdf
www.mat.uel.br/geometrica/php/pdf/dg_prop_áurea.pdf
www.unemat.br/faciex/professores/nelo/arquivos/curso_geometria/razao_aurea_pentago_regular.pdf
Postar um comentário