PROJETO 002/09
TÍTULO: NÚMEROS NOTÁVEIS
COORDENADOR: ALEXANDER PEREIRA
ETAPA P-2
Definição (se possível) da cronologia de surgimento e aplicação do “e”.
O número e e o logaritmo
A 1ª noção do e aparece no estudo dos logaritmos de John Napier (1550-1617). Napier parece ter apresentado o valor de

para

que é aproximadamente

Num apêndice, provavelmente escrito por William Oughtred (1574-1660), de uma tradução do trabalho de Napier feita por Edward Wright (1618) aparece o valor

Esta parece ser a 1ª aparição do e no cenário matemático.
Em 1624, o e esteve para voltar ao cenário matemático quando Briggs apresentou uma aproximação numérica do logaritmo de e na base 10; porém fez isso sem mencionar o e.
O número e e a hipérbole retangular
Em 1647, Gregorius de Saint-Vicent (1584 – 1667) ao calcular a área sob uma hipérbole retangular, provavelmente se deparou com o número e, porém não se tem certeza se ele fez a conexão entre a hipérbole retangular e os logaritmos, já que não haviam razões práticas para que fosse estabelecida esta conexão.
Finalmente, em 1661, Christiaan Huygens (1629 – 1695) compreendeu a relação entre a área sob a hipérbole

e os logaritmos. O número
e é tal que a área sob a hipérbole, entre 1 e
e é igual a 1. Ainda neste ano, Huygens definiu uma curva que chamou de “logarítmica”, mas que na terminologia moderna seria “curva exponencial”. Esta curva estava associada a funções do tipo

Com essa curva, ele apresentou um valor para o logaritmo decimal de e com 17 casas decimais. Porém, este valor foi apresentado como uma constante e não como o logaritmo de um número, adiando o reconhecimento de
e.
Em 1668, Nicolaus Mercátor (1620 – 1687) publica Logarithmotechnia, onde aparece a expansão em séries de

Pela primeira vez, é utilizado o termo “logaritmo natural”. Mais uma vez, o
e não é apresentado de forma explícita.
O número e e os juros compostos
Jacob (Jacques) Bernoulli (1654 – 1705) apresentou o que é considerado a primeira definição de
e: um número entre 2 e 3 que é resultado de

quando n tende ao infinito. Este valor está ligado a um problema de juros compostos com capitalização “instantânea”. Esta definição, curiosamente, não está relacionada aos trabalhos sobre logaritmos citados anteriormente.
A primeira aparição explícita acontece em 1690. Numa carta de Gottfried Wilhelm von Liebniz (1646 – 1716) para Huygens é utilizada a notação
b para o nosso atual
e.
O número
e, Euler e a irracionalidade
Durante o século XVIII, Leonhard Euler (1707-1783) deu uma consistência rigorosa a definição do
e. Também é creditado a Euler o batismo deste número como
e. Porém, é improvável que ele tenha pensado na inicial do seu sobrenome para representar este curioso número. Esta representação aparece pela primeira vez, em 1731, numa carta de Euler à Christian Goldbach (1690 – 1764).
Ele derivou o desenvolvimento binomial, concluindo, em 1748 no seu Introductio in Analysin infinitorum, que:

Este resultado, Euler verificou que também era a base dos logaritmos hiperbólicos. Euler utilizou a relação

para escrever e com 23 casas decimais.
Em “De fractionibus continuis dissertatio”, 1737, L. Euler demonstrou que o número e tem expansão em frações contínuas simples da forma [1, 0, 1, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, . . .].
A irracionalidade de e foi demonstrada por Johann Heinrich Lambert (1728 – 1777) em 1761 e mais tarde por Euler.
Em 1815, J.B. Fourier deu uma prova simples da irracionalidade de e por meio de séries.
O número e, casas decimais e transcendência
O primeiro a apresentar o e com um número grande de casas decimais foi William Shanks (1812 – 1882), em 1854. James Whitbread Lee Glaisher (1848 – 1928) mostrou que as 137 primeiras casas do desenvolvimento de Shanks estavam corretas, porém havia um erro. Corrigido este erro, Shanks apresentou o e com 205 casas decimais.
Em 1864, surge uma gravura com Benjamin Peirce (1809 – 1880) em frente a um quadro-negro onde está anotada a fórmula:

Durante suas aulas, ele dizia para seus alunos que este era um resultado muito importante apesar de não saber exatamente o que significava.
Em 1873, Charles Hermite publica “Sur la fonction exponentielle”, no qual apresenta a prova da transcendência de e. Continua em aberto a prova de transcendência de

apesar de nenhum matemático duvidar deste fato.
Em 1884, Boorman calculou e com 346 casas decimais, verificando que seu resultado coincidia com o de Shanks até 187 casas e, depois, variavam. Adams calculou o logaritmo decimal de e com 272 casas decimais, em 1887.


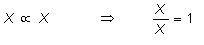



 para
para que é aproximadamente
que é aproximadamente

 e os logaritmos. O número e é tal que a área sob a hipérbole, entre 1 e e é igual a 1. Ainda neste ano, Huygens definiu uma curva que chamou de “logarítmica”, mas que na terminologia moderna seria “curva exponencial”. Esta curva estava associada a funções do tipo
e os logaritmos. O número e é tal que a área sob a hipérbole, entre 1 e e é igual a 1. Ainda neste ano, Huygens definiu uma curva que chamou de “logarítmica”, mas que na terminologia moderna seria “curva exponencial”. Esta curva estava associada a funções do tipo Com essa curva, ele apresentou um valor para o logaritmo decimal de e com 17 casas decimais. Porém, este valor foi apresentado como uma constante e não como o logaritmo de um número, adiando o reconhecimento de e.
Com essa curva, ele apresentou um valor para o logaritmo decimal de e com 17 casas decimais. Porém, este valor foi apresentado como uma constante e não como o logaritmo de um número, adiando o reconhecimento de e. Pela primeira vez, é utilizado o termo “logaritmo natural”. Mais uma vez, o e não é apresentado de forma explícita.
Pela primeira vez, é utilizado o termo “logaritmo natural”. Mais uma vez, o e não é apresentado de forma explícita. quando n tende ao infinito. Este valor está ligado a um problema de juros compostos com capitalização “instantânea”. Esta definição, curiosamente, não está relacionada aos trabalhos sobre logaritmos citados anteriormente.
quando n tende ao infinito. Este valor está ligado a um problema de juros compostos com capitalização “instantânea”. Esta definição, curiosamente, não está relacionada aos trabalhos sobre logaritmos citados anteriormente. Este resultado, Euler verificou que também era a base dos logaritmos hiperbólicos. Euler utilizou a relação
Este resultado, Euler verificou que também era a base dos logaritmos hiperbólicos. Euler utilizou a relação


